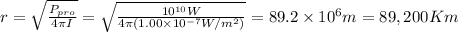Answer:
a) The pressure amplitude at this distance is
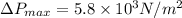
b) The displacement amplitude is

c) The distance at which the sound intensity level drops to 50 dB is
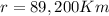
Step-by-step explanation:
a) We need to convert to dB to watts, so
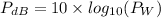 , then
, then
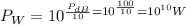 .
.
Then we can find Intensity at 100m, so
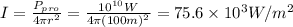 .
.
And finally, the pressure amplitude at this distance will be
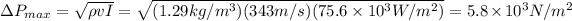
b) Using
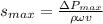 , with
, with
 , thus,
, thus,
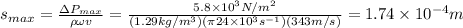
c) We need to find intensity, so
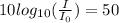 , then,
, then,
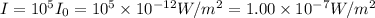 .
.
Finally, the distance at which the sound intensity level drops to 50 dB will be