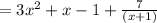The result in form of q(x) + r(x)/b(x) is
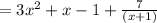
Solution:
Need to divide
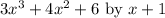
The image for the division is attached below
Step 1: here x + 1 is dividend and
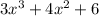 is divisor
is divisor
Step 2: Divide the first term of numerator by first term of denominator and place it in quotient
Step 3: Multiply the denominator by that answer and put that below the numerator
Step 4: Subtract to obtain a new polynomial
Step 5: Repeat using the new polynomial until no variable “x’ is left in remainder
On dividing we get quotient q(x)
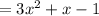 remainder r = 7 and dividend b(x) = x+1
remainder r = 7 and dividend b(x) = x+1
Expressing it in
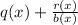 we get,
we get,