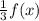Answer:
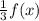
Explanation:
In this case the transformation being done to the graph of f is a dilation. To find the value that is dilating the graph, you can compare 2 points. First, figure out what axis is changing. In this example, we can see that the y values changed. That means that the value that dilates the graph is outside of the function f(x) as it is modifying the output. Since it's only the y-values changing, we need to grab 2 points with the same x values but differents y values. The 2 points that make this the easiest are (2,-3) on f and (2,-1) on g. If we compare the 2, we see that the y-values between f and g changed. If we were to make a ratio of the change, we would get:
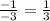
Therefore, the dilation factor is one third. This is being applied to the y-values so it is placed outside the function, meaning that the answer is: