Question

Two bottling plants package a certain type of sports drink. Suppose the mean volume of all of this type of sports drinks is 20 fluid ounces. Bottling plant A bottles approximately 43607 sports drinks per day. Bottling plant B bottles approximately 179811 sports drinks per day. On a particular day, which bottling plant is less likely to record a mean volume of 21 fluid ounces for the day? A. The two bottling plants are equally likely to record such a volume because random samples from both plants will have daily mean volumes that vary.

B. Bottling plant A (with 50,000 sports drinks per day), because with fewer sports drinks there will be less variability in the daily mean volume.

C. Bottling plant B (with 175,000 sports drinks per day), because the daily mean will be closer to 20 fluid ounces with more sports drinks in the sample.

Answer 1

C. Bottling plant B (with 175,000 sports drinks per day), because the daily mean will be closer to 20 fluid ounces with more sports drinks in the sample.

Explanation:

The general rule is that the larger the sample, the closer the sample mean will be to the population mean. This happens because the standard deviation of our sample is given by the following formula:

`s = (\sigma)/(√(n))`

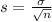
In which
`\sigma` is the standard deviation of the mean volume of all of this type of sports drinks and
`n` is the size of the sample. So as
`n` increases, the less variation there will be, and the closer the sample mean will be to the population mean, that is, the closer the population mean is going to be closer to a mean volue of 20 fluid ounces.

So, the correct answer is:

C. Bottling plant B (with 175,000 sports drinks per day), because the daily mean will be closer to 20 fluid ounces with more sports drinks in the sample.