Question

two friends drive from dallas going to el paso, a distance of 600 miles. mary ann zilke travels by highway and arrives at the same destination 2 hours ahead of carla canola, who took a different route. if the average speed of mary ann's car was 10 miles per hour faster than carla's car, find the average speed of each car​

Answer 1

The average speed of Carla and mary is 50 and 60 miles per hour respectively.

SOLUTION:

Given, Two friends drive from dallas going to el paso, a distance of 600 miles.

mary and zilke travels by highway and arrives at the same destination 2 hours ahead of carla canola

The average speed of mary ann's car was 10 miles per hour faster than carla's car,

We have to find the average speed of each car?

Now, let the speed of Carla be s miles per hour, then speed of mary will be s + 10 miles per hour.

And let the time taken by Carla be t, then time taken by mary will be t – 2 hours

Now, we know that, distance = speed x time

Then, for mary ⇒ 600 miles =
`( s + 10 ) * (t - 2)`

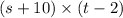
And for Carla ⇒ 600 miles =
`s * t`

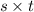
Now, equate both the equations.

(s + 10) (t – 2) = st ⇒ s(t – 2) + 10(t – 2) = st

St – 2s + 10t – 20 = st

2s – 10t + 20 = 0

s – 5t + 10 = 0

since
`s * t = 600` the above equation becomes,

`\mathrm{s}-5 * (600)/(s)+10=0`

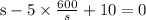
By multiplying equation with s,

`\begin{array}{l}{s^(2)+10 s-3000=0} \\\\ {s^(2)+60 s-50 s-3000=0} \\\\ {s(s+60)-50(s+60)=0} \\\\ {(s+60)(s-50)=0}\end{array}`

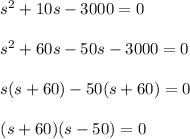
s = 50 or -60 [ neglect –ve values, as speed can't be negative]

So, speed of Carla is 50 miles per hour, then speed of mary is 50 + 10 = 60 miles per hour.

Hence, the average speed of Carla and mary is 50 and 60 miles per hour respectively.