Question

Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If the graph of f is concave upward on (a, c) and concave downward on (c, b), where a < c < b, then f has an inflection point at x = c.

Answer 1

False.

Explanation:

Remember the following:

Definition 1: (Concavity of a function) Let f be a real valued function. If the graph of f lies above all of its tangents on an interval I, then it is called concave upward on I. If the graph of f lies below all of its tangents on an interval I, then is called concave downward on I.

Concavity test:

1. If f''(x)>0 for all x in I, then the graph of f is concave upward on I.
2. If f''(x)<0 for all x in I, then the graph of f is concave downward on I.

Definition 2: (Inflection point) A point P on a curve y=f(x) is called an inflection point if f is continuous there and the curve changes from concave upward to concave downward or from concave downward to concave upward at P.

Knowing this, the important condition here is that of continuity of the function f at the point P.

We are going to construct a function satisfying almost every condition given in definition 2, except that of the continuity at a specific point where it changes its concavity.

Let f the function defined by
`f(x)=\begin{cases}\hfil -x^3, & x\leqslant 0, \\ 1-x^3, & x>0. \end{cases}`

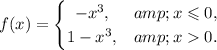
Then, by the concavity test, we see that for x < 0,
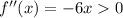`f''(x)= -6x >0`, and so f is concave upward, and for x > 0,
`f''(x)=-6x < 0`, and hence f is concave downward. Nevertheless, f is not continuous at x = 0 since
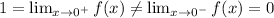`1= \lim_(x \to 0^+) f(x) \\eq \lim_(x \to 0^-) f(x)=0`. Therefore there is no inflection point at x = 0.

In conclusion, the statement is FALSE