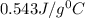Answer:
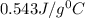
Step-by-step explanation:
Volume of metal = volume of water displaced = (30.0 - 25.0) ml = 5.0 ml
Density of metal = 5.50 g/ml
Mass of metal =
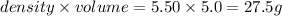
Volume of water = 25.0 ml
Density of metal = 1.0 g/ml
Mass of metal =

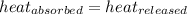
As we know that,
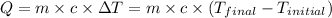
![-[m_1* c_1* (T_(final)-T_1)]=[m_2* c_2* (T_(final)-T_2)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/2tq5z1j9loloeb53rj9rh3fw8abt3yk5sb.png) .................(1)
.................(1)
where,
q = heat absorbed or released
 = mass of metal = 27.5 g
= mass of metal = 27.5 g
 = mass of water = 25.0 g
= mass of water = 25.0 g
 = final temperature = ?
= final temperature = ?
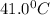
 = temperature of metal =
= temperature of metal =
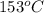
 = temperature of water =
= temperature of water =
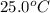
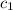 = specific heat of lead = ?
= specific heat of lead = ?
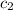 = specific heat of water=
= specific heat of water=
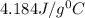
Now put all the given values in equation (1), we get
![27.5g* c_1* (41.0-153)^0C=[25.0g* 4.814J/g^0C* (41.0-25.0)^0C]](https://img.qammunity.org/2020/formulas/chemistry/high-school/tccnonbepbb02q5jmoygu5k7qmc98cbkvb.png)
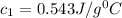
Thus the specific heat of the unknown metal sample is