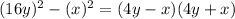Question

Which shows a difference of squares?

10 y squared minus 4 x squared
16 y squared minus x squared
8 x squared minus 40 x + 25
64 x squared minus 48 x + 9

Answer 1

B. 16y squared-x squared

Explanation:

Took the test got a 100%

Good luck:)

Answer 2

The expression which shows the difference of squares is
`(16y)^(2)  - (x)^(2)` .

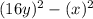Explanation:

Here, the given expressions are :

`1. (10y)^(2)  - (4x)^(2)\\2.(16y)^(2)  - (x)^(2)\\3. (8x)^(2)  - (4x + 25)\\4. (64x)^(2)  - (48x + 9)`

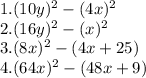
Now, DIFFERENCE of SQUARES is an expression where one perfect square term is subtracted from another perfect square term.

And each difference of square can be expanded using algebraic identity

`a^(2) - b^(2)  = (a-b)(a+b)`

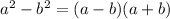
Now, here only the terms in expression 2 are perfect squares, as

`(16y)^(2)  = (4y)^(2) =(-4y)^(2)  , (x)^(2)  = (x)^(2) =(-x)^(2)`

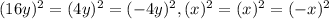
Hence, the expression which shows the difference of squares is
`(16y)^(2)  - (x)^(2)` .

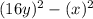Also, here
`(16y)^(2) - (x)^(2)  = (4y-x)(4y+x)`