Question

The power generated by an electrical circuit (in watts) as a function of its current ccc (in amperes) is modeled by: P(c)=-12c^2+120cP(c)=?12c 2 +120cP, left parenthesis, c, right parenthesis, equals, minus, 12, c, start superscript, 2, end superscript, plus, 120, c What current will produce the maximum power?

Answer 1

5 amperes will produce the maximum power of 300 watts.

Explanation:

The general form of a quadratic function presents the function in the form

`f(x)=ax^2+bx+c`

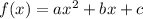
The vertex of a quadratic function is the highest or lowest point, also known as the maximum or minimum of a quadratic function.

We can define the vertex by doing the following:

• Identify a, b, and c
• Find, the x-coordinate of the vertex, by substituting a and b into

`x-coordinate =-(b)/(2a)`

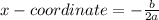
• Find, the y-coordinate of the vertex, by evaluating

`y-coordinate =f(x-coordinate )=f(-(b)/(2a) )`

We know that the power generated by an electrical circuit is modeled by

`P(c)=-12c^(2)+120c`

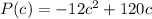
This function is a quadratic function.

To find the current that produce the maximum power you must

• Identify a and b

a = -12 and b = 120

• Find, the maximum current of the vertex, by substituting a and b into

`maximum-current =-(b)/(2a)`

`maximum-current =-(120)/(2(-12))\\\\maximum-current = 5`

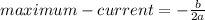
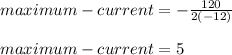
• Find, the maximum-power, by evaluating

`maximum-power =P(maximum-current)=P(-(b)/(2a) )`

`P(5)=-12(5)^(2)+120(5)=300`

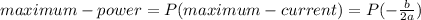
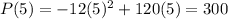
5 amperes will produce the maximum power of 300 watts.

We can check our work with the graph of the function
`P(c)=-12c^(2)+120c` and see that the maximum is (5, 300).