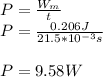Question

The electric motor of a model train accelerates the train from rest to 0.685 m/s in 21.5 ms. The total mass of the train is 875 g. Find the minimum power delivered to the train by electrical transmission from the metal rails during the acceleration.

Answer 1

P=9.58 W

Step-by-step explanation:

According to Newton's second law, and assuming friction force as zero:

`F_m=m.a\\F_m=0.875kg*a`

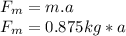
The acceleration is given by:

`a=(\Delta v)/(t)\\a=(0.685m/s)/(21.5*10^(-3)s)\\\\a=31.9m/s^2`

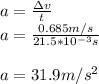
So the force exerted by the motor is:

`F_m=0.875kg*31.9m/s^2\\F_m=27.9N`

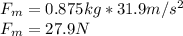
The work done by the motor is given by:

`W_m=F_m*d\\\\d=(1)/(2)*a*t^2\\d=(1)/(2)*31.9m/s^2*(21.5*10^(-3)s)^2\\\\d=7.37*10^(-3)m`

`W_m=27.9N*7.37*10^(-3)m\\W_m=0.206J`

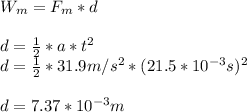
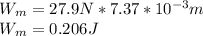
And finally, the power is given by:

`P=(W_m)/(t)\\P=(0.206J)/(21.5*10^(-3)s)\\\\P=9.58W`