Question

A cube has an edge of 4 feet. The edge is increasing at the rate of 3 feet per minute. Express the volume of the cube as a function of m, the number of minutes elapsed

Answer 1

V = 144m + 64

Explanation:

The cube has an edge (a) = 4 feet.

Now, the volume of the cube is given by V = a³ ....... (1)

So, initially, the volume of the cube was 4³ =64 cubic feet.

Now, differentiating equation (1) with respect to m (a variable which measurea number of minutes) we get

`(dV)/(dm) = 3a^(2) (da)/(dm) =3 * 4^(2)  * 3 =144`

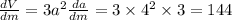
{Since the rate of change of length of edge is 3 feet/ minutes}

⇒
`dV = 144 * dt`

Integrating both sides we get,

V = 144m + c {Where c is the constant of integration} ........ (2)

Now, we know that at m = 0, V = 64 cubic feet.

So, from equation (2), we get c = 64

Therefore, V = 144m + 64 .... this is the expression of V in terms of m. (Answer)