Answer:

 (impact)
(impact)
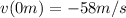 (impact)
(impact)
Step-by-step explanation:
The equation for height is
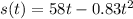
We derive the equations for velocity and acceleration by derivating it respect with time:
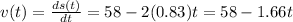
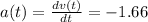
So we have (adding units at the end):
The velocity after 7s (evaluating the velocity formula for 7):
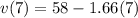
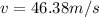
The time it hits the moon (when the height is null again):
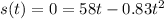
One solution is t=0, which corresponds to departure of course, but we want the other solution, which is for impact.

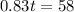
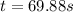
The velocity at the time it hits the moon:
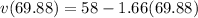
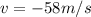
As it should be since the arrow left the moon at 58m/s.