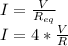Question

A resistor is made out of a long wire having a length L. Each end of the wire is attached to a terminal of a battery providing a constant voltage V0. A current I flows through the wire. If the wire were cut in half, making two wires of length L/2, and both wires were attached to the battery (the end of both wires attached to one terminal, and the other ends attached to the other terminal), what would be the total current flowing through the two wires?

Answer 1

The current is 4 times the current of the full length wire.

Step-by-step explanation:

The resistor value is directly proportional to its length:

`R=\rho *(L)/(A)`

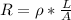
the current is given by:

`I=(V)/(R)`

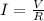
so if the wire was cut in the half:

`R_n=\rho *(L)/(2*A)=(1)/(2)*\rho *(L)/(A)=(1)/(2)R`

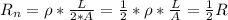
Both ends of the wire were connected to the battery, so they are connected in parallel, the equivalent resistor is given by:

`R_(eq)=(1)/((1)/(R_n)+(1)/(R_n))=(1)/((1)/((R)/(2))+(1)/((R)/(2)))\\\\R_(eq)=(R^2)/(4R)=(R)/(4)`

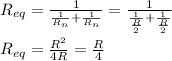
So the current is:

`I=(V)/(R_(eq))\\I=4*(V)/(R)`