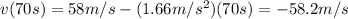Answer:
a)
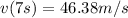
b)
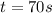
c)
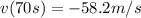
Step-by-step explanation:
From the exercise we know the arrow's equation of position
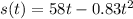
a) If we want to know the velocity of the arrow after t=7s we need to derivate the equation of position to get velocity
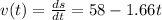
Now, we evaluate 7s in the equation
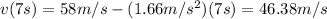
b) To find how much time does it take the arrow to hit the moon we need to evaluate s=0 at the equation of position in the vertical direction
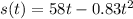
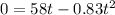
Solving the quadratic equation using the following formula
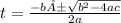
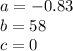
 or
or
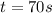
Since time can not be zero the answer is t=70s
c) To calculate the arrow's velocity when it hits the moon we need to evaluate t=70s in the equation of velocity