The worth of investment after 25 years is $17545419.8 approximately.
Solution:
Given, If $4,000,000 is invested at 5% interest compounded continuously,
We have to find how much will the investment be worth in 25 years?
The formula for Compound interest is given as:
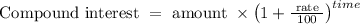
Substituting the values we get,

Now, investment worth after 25 years = invested amount + compound interest
= 4000000 + 13545419.7636 = 17545419.7636
Hence, the worth of investment after 25 years is $17545419.8 approximately.