Question

The temperature at the bottom of a reservoir is TL = 280 K and the surface temperature is TH = 295 K. This temperature difference is used to run a steadystate power cycle that develops a power output of 8 kW, while rejecting energy by heat transfer at the rate 14,400 kJ/min. Determine: (a) The thermal efficiency of the power cycle, in %. (b) The maximum thermal efficiency for any such power

Answer 1

a) For the thermal efficiency we have

`\eta_(th) = (Q_(out))/(Q_(in)) = (|W|)/(|Q_h|)\\\eta_(th) = (|W|)/(|W|+|Q_2|)`

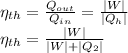
With the previously values we know that

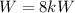`W=8kW` and
`Q_L = 1440/6kW` (convert the min to sec)

Replacing the values

`\eta_(th)=(8)/(8+1440/6)=(1)/(31)\\\eta_(th)\% = 3.225\%`

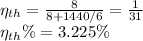
b) We use the formula of carnot efficiency

`\eta_(th)=1-(T_l)/(T_h)\\\eta_(th)\% =(1-(280)/(295))*100\\\eta_(th)\%=5.085\%`

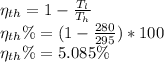
**Note that apply the formula of carnot cycle we need to consider that there is no exchange of heat, there is no friction and the reservior are completely insulated