Question

A horizontal wire is stretched with a tension of 96.4 N, and the speed of transverse waves for the wire is 401 m/s. What must the amplitude of a traveling wave of frequency 68.4 Hz be for the average power carried by the wave to be 0.392 W? Give an answer in mm. Pay attention to the number of significant figures.

Answer 1

Amplitude will be
`A=8.3731* 10^(-3)m`

Step-by-step explanation:

We have given tension in the string T = 96.4 N

Power carried by the wave P = 0.392 W

Frequency of the wave f = 68.4 Hz

Velocity of the wave v = 401 m/sec

We know that velocity of transverse wave is given by
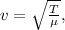`v=\sqrt{(T)/(\mu )},` here T is tension and
`\mu` is mass per length

So
`401=\sqrt{(96.4)/(\mu )}`

`\mu =6* 10^(-4)kg/m`

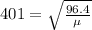
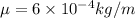
Now angular frequency is given by
`\omega =2\pi f=2* 3.14* 68.4=429.552rad/sec`

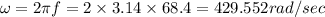
Now power is given by

`P=(1)/(2)\mu A^2\omega ^2v`

So
`0.392=(1)/(2)* 6* 10^(-4)* A^2* 429.552^2* 401`

`A=8.3731* 10^(-3)m`