Question

Unit Test

Active
INL KEMA
01:14
Use the zero product property to find the solutions to the equation x² + x - 30 = 12.
x = -7 or x = 6
x= -7 or x = -6
x = -6 or x = 7
Ox= 6 or x = 7

Answer 1

x = -6, or x = 7 is the ONLY correct solution of the given equation
`x^(2)  + x - 30 = 12.`

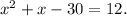
Explanation:

Here, the given expression is
`x^(2)  + x - 30 = 12.`

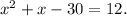
or the standard form of the above expression is
`x^(2)  + x - 30 -  12 = 0`

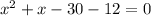
or,
`x^(2)  + x - 42 = 0`

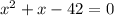
Now, if the equation is of the form
`ax^(2)  + bx + c = 0`

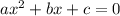
Then, b = SUM OF THE ROOTS

and c = PRODUCT OF THE ROOTS

Similarly, in the above expression:

b = 1 = Sum of roots

and c = -42 = Product of the roots.

Here, for x = -6, or x = 7:

Sum of Roots = -6 + 7 = 1

Product of roots = (-6)(7) = -42

Hence, x = -6, or x = 7 is the ONLY correct solution of the given equation.