Answer: B . 0.9615
Explanation:
Explanation:
Let x be a random variable that represents the lengths of the shells .
As per given , we have
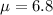 inches
inches
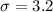 inches
inches
n= 50
∵
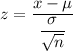
Then for x= 6,
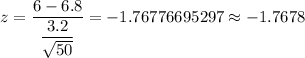
The probability the sample means would we expect to be greater than 6 inches :-
![P(x>6)=P(z>-1.7678)=P(z<1.7678)\ \ [\because P(Z>-z)=P(Z<z)]\\\\=0.9614528\approx0.9615](https://img.qammunity.org/2020/formulas/mathematics/college/cntdagphmbt438ss3wr7lm5h1fpd42rj2a.png) [using the z values table]
[using the z values table]
Hence, the proportion of the sample means would we expect to be greater than 6 inches = 0.9615