Question

What are the vertical and horizontal asymptotes for the function f (x) =
`(x^(2)+x-6 )/(x^(3)-1)`

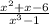
A. vertical asymptote: x = 1

horizontal asymptote: none

B. vertical asymptote: x = 1

horizontal asymptote: y = 0

C. vertical asymptote: x = –2, x = 3

horizontal asymptote: y = 0

D. vertical asymptote: x = –2, x = –3

horizontal asymptote: none

Answer 1

B. vertical asymptote: x = 1

horizontal asymptote: y = 0

Explanation:

1) Vertical asymptotes of a function are determined by what input of x makes the denominator equal 0. So, let's set the denominator,
`x^3-1`, equal to 0 and solve for x:

`x^3-1= 0\\x^3 = 1\\\sqrt[3]{x^3} = \sqrt[3]{1} \\x = 1`

Thus, the vertical asymptote is x = 1.

2) If the degree of the polynomial in the denominator is greater than the one on the top, the horizontal asymptote is automatically y = 0. Thus, the horizontal asymptote is y = 0.

Answer 2

B. x=1, y=0

Explanation:

Vertical asymptote: denominator approximate 0

(x²+x-6)/(x³-1) ---> ±∞ as x ---> 1

x³-1 = 0

x³ = 1

x = ∛1 = 1

Horizontal asymptote: If the degree of the numerator is less than the degree of the denominator, then the horizontal asymptote is always the x axis, i.e. the line y = 0

degree of the numerator: 2

degree of the denominator: 3

2<3

Horizontal asymptote: y = 0