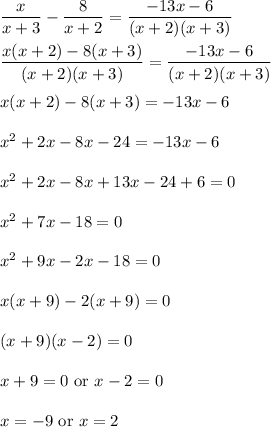Question

(x/x+3)-(8/x+2)=(-13x-6)/(x^2+5x+6)​

Answer 1

x = -9

x = 2

Explanation:

Given:

`(x)/(x+3)-(8)/(x+2)=(-13x-6)/(x^2+5x+6)`

First, note that

`x^2+5x+6=x^2+2x+3x+6=x(x+2)+3(x+2)=(x+2)(x+3)`

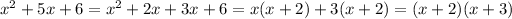
Since
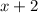`x+2` and
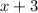`x+3` stay in the denominator, then

`x\\eq -2\ \text{and}\ x\\eq -3`

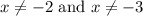
Now add two fractions which stay in the left part. The common denominator is
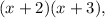`(x+2)(x+3),` so multiply the numerator of the first fraction by
`(x+2)` and the numerator of the second fraction by
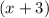`(x+3)` and subtract them in the numerator:

`(x)/(x+3)-(8)/(x+2)=(-13x-6)/((x+2)(x+3))\\ \\(x(x+2)-8(x+3))/((x+2)(x+3))=(-13x-6)/((x+2)(x+3))\\ \\x(x+2)-8(x+3)=-13x-6\\ \\x^2+2x-8x-24=-13x-6\\ \\x^2+2x-8x+13x-24+6=0\\ \\x^2+7x-18=0\\ \\x^2+9x-2x-18=0\\ \\x(x+9)-2(x+9)=0\\ \\(x+9)(x-2)=0\\ \\x+9=0\ \text{or}\ x-2=0\\ \\x=-9\ \text{or}\ x=2`