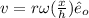Question

A viscous liquid is sheared between two parallel disks of radius �, one of which rotates with angular speed Ω, while the other is fixed. The velocity field is purely tangential, and the velocity varies linearly with z from: �; = 0 at � = 0 (the fixed disk) to the velocity of the rotating disk at its surface (� = ℎ). Derive an expression for the velocity field between the disks.

Answer 1

Upper disk rotates at a constant angular velocity. The velocity at any height from stationery disk, say at x metres

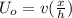`U_o=v(\frac {x}{h})` where v is tangential velocity at radius r from the centre of disk

`U_o=r\omega (\frac {x}{h})`

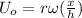
The radial component of velocity is given as

`U_r=0`

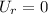
The z component of velocity is also given as

W=0

Total velocity,
`v= r\omega (\frac {x}{h})\hat e_(o)`