Answer:
The center has the coordinates
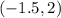 and the radius 2.5
and the radius 2.5
Explanation:
Let
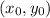 be the center of the circel and r be the radius, then the equation of the circle is
be the center of the circel and r be the radius, then the equation of the circle is
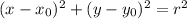
Circle O with center
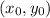 passes through the points A(0,0), B(-3,0), and C(1, 2), so
passes through the points A(0,0), B(-3,0), and C(1, 2), so
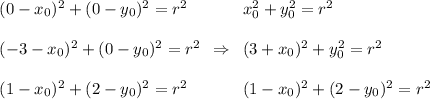
Subtract from the second equation the first one:
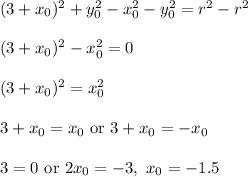
Substitute it into the last two equations:
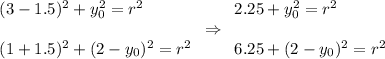
Subtract them:
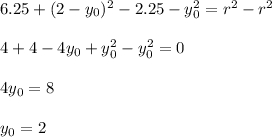
Substitute into the first equation:
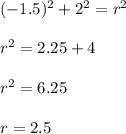
So, the center has the coordinates
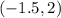 and the radius 2.5
and the radius 2.5