Question

An article reported that, in a study of a particular wafer inspection process, 356 dies were examined by an inspection probe and 229 of these passed the probe. Assuming a stable process, calculate a 95% (two-sided) confidence interval for the proportion of all dies that pass the probe. (Round your answers to three decimal places.)

Answer 1

[0.5935, 0.6930]

Explanation:

The 95% confidence interval is given by

`\bf p\pm t^*√(p(1-p)/n)`

where

p = the proportion of dies that passed the probe = 229/356 = 0.6432

`\bf t^*` the Student's t distribution value for a 95% confidence level and 355 degrees of freedom (sample size -1)

n = sample size

Since the sample size is big enough,
`\bf t^*` equals the value
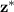`\bf z^*` for the 95% confidence level associated with the Normal distribution N(0,1)
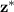`\bf z^*` = 1.96

This value can be found either with a table or with a spreadsheet.

In Excel use NORM.INV(0.975,0,1)

In OpenOffice Calc use NORMINV(0.975;0;1)

We get a value of
`\bf z*`= 1.96

and our 95% confidence interval is

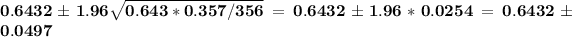`\bf 0.6432\pm 1.96√(0.643*0.357/356)=0.6432\pm 1.96*0.0254=0.6432\pm 0.0497` = [0.5935, 0.6930]

To interpret this result, we could say there is a 95% of probability that the proportion of dies that should pass the inspection process is between 59.35% and 69.30%