Question

In a random sample of fivefive microwave​ ovens, the mean repair cost was ​$75.0075.00 and the standard deviation was ​$13.0013.00. Assume the population is normally distributed and use a​ t-distribution to construct a 9090​% confidence interval for the population mean muμ. What is the margin of error of muμ​? Interpret the results.

Answer 1

Answer with explanation:

As per given , we have

Sample size : n= 5

Degree pf freedom = : df= 5-1=4

`\mu=\$75.00`

`\sigma=\$13.00`

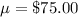
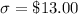
Significance level for 90% confidence =
`\alpha=1-0.90=0.1`

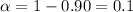
Using t-value table , t-critical value for 90% confidence:

`t_(\alpha/2, df)=t_(0.05, 4)=2.132.`

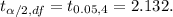
Margin of error of
`\mu`:
`E=t_(\alpha/2)(\sigma)/(√(n))\\\\(2.132)(13)/(√(5))=12.3949720129\approx12.39`

Interpretation : The repair cost will be within $12.39 of the real population mean value
`\mu` 90% of the time.