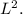Question

A wire of length L is cut at the red point. The segment to the left of the cut is formed into an equilateral triangle, and the segment to the right of the cut is formed into a square. Let x be the length of the segment to the left of the cut.

(a)-What value of x maximizes the total area of the two shapes?
(b)-What value of x minimizes the total area?

Answer 1

`(a) x=0\\(b)\ x=(4L)/(4+√(3))`

Explanation:

Imagine that the wire is cut as shown in the picture. We know that the lenght of the segment to the left is
`x` and therefore the lenght of the segment to the right must be
`L-x.`

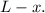
Using the formula for the area of an equilateral triangle of sides of length x, we get that
`A_(\bigtriangleup)(x)=(√(3))/(4)\, x^2.`

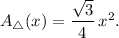
And using the formula for the area of a square of length L-x, we obtain that
`A_(\square)(x)=(L-x)^2.`

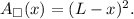
Then, the total area of the two shapes is giving by the sum of both areas:
`A_T(x)=A_(\bigtriangleup)(x)+A_(\square)(x)=(√(3))/(4)\, x^2 + (L-x)^2.`

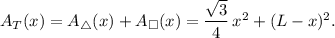
Now we have to find the values x where the function
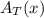`A_T(x)` attains its maximum and its minimum. For this purpose, we calculate its critical points, which occurs when the derivative vanishes:

`A_T'(x)=A_(\bigtriangleup)'(x)+A_(\square)'(x)=(√(3))/(2)x-2(L-x)=0.`

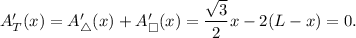
Solving for x we get that:

`x=(4L)/(4+√(3)).`

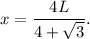
This is the only critical point. Using the second derivative test we found that, since
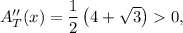`A_T''(x)=(1)/(2) \left(4 + √(3)\right) >0,` then at
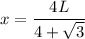`x=(4L)/(4+√(3))` the area of the two shapes is minimized.

Now, the only way we have maximum area is when the red point is on the extreme of the wire, at x = 0. This because in that situation, there is no triangle that can be formed and therefore the area is equals
`L^2.`