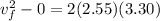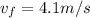Answer:
Part a)
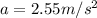
Part b)
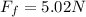
Part c)
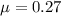
Part d)
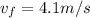
Step-by-step explanation:
Part a)
As we know that the length of the slide is L = 3.30 m
time = 1.61 s
so we can use kinematics here to find the acceleration of the bag
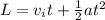

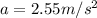
Part b)
As we know by force equation
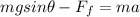
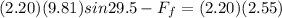
so we have
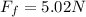
Part c)
Now we know that perpendicular to the plane we will have
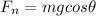
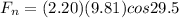
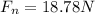
now we know that
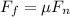
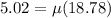
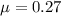
Part d)
When the bag will reach at the bottom then the final speed is given as
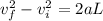
so we have