Answer: 0.8413
Explanation:
Explanation:
Let x be a random variable that represents the life span of monitors manufactured by TSI Electronics .
Also Monitors manufactured by TSI Electronics have life spans that have a normal distribution with
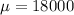 hours
hours
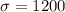 hours
hours
∵

Then for x= 16,800 hours,
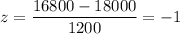
The probability that the life span of the monitor will be more than 16,800 hours. :-
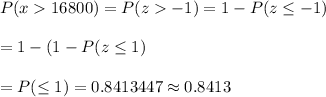
Hence, he probability that the life span of the monitor will be more than 16,800 hours = 0.8413