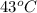Question

Enter your answer and show all the steps that you use to solve this problem in the space provided. Find the values of x and y.

Answer 1

Answer : The value of x and y is,
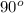`90^o` and
`43^oC`

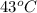
Step-by-step explanation :

First we have to calculate the angle B.

As we know that,

The given triangle is an isosceles triangle in which the angles opposite to equal sides are always equal.

Thus,
`\angle B=\angle C`

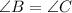
Given :
`\angle C=47^o`

`\angle B=\angle C=47^o`

`\angle B=47^o`

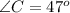
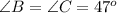
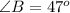
Now have to calculate the angle A.

As we know that the sum of interior angles of a triangle is equal to
`180^o`.

`\angle A+\angle B+\angle C=180^o`

`\angle A+47^o+47^o=180^o`

`\angle A+94^o=180^o`

`\angle A=180^o-94^o`

`\angle A=86^o`

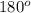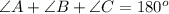
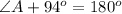
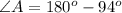
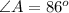
Now we have to determine the angle y.

As we know that, line AD is an angle bisector. That means, it divides into two equal angles. So,

`\angle y=(\angle A)/(2)`

`\angle y=(86^o)/(2)`

`\angle y=43^o`

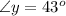
Now we have to determine the angle x.

As we know that the sum of interior angles of a triangle is equal to
`180^o`.

`\angle y+\angle B+\angle x=180^o`

`43^oc+47^o+\angle x=180^o`

`\angle x+90^o=180^o`

`\angle x=180^o-90^o`

`\angle x=90^o`

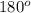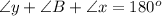
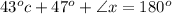
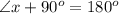
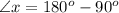
Thus, the value of x and y is,
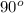`90^o` and
`43^oC`