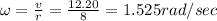Question

A fairground ride spins its occupants inside a flying saucer-shaped container. If the horizontal circular path the riders follow has an 8.00 m radius, (a) at what angular velocity (in rad/s) will the riders be subjected to a centripetal acceleration 1.9 times that due to gravity?

Answer 1

Angular velocity will be 1.525 rad/sec

Step-by-step explanation:

We have given radius of the circular path r = 8 m

We have given centripetal acceleration
`\alpha =1.9g=1.9* 9.8=18.62m/sec^2`

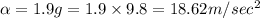
Now we know that centripetal acceleration is given by
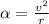`\alpha =(v^2)/(r)`, here v is linear velocity and r is radius

So
`18.62 =(v^2)/(8)`

v = 12.204 m/sec

Now we know that linear velocity is given by
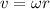`v=\omega r`, here
`\omega` is angular velocity and r is radius

So
`\omega =(v)/(r)=(12.20)/(8)=1.525rad/sec`