Question

A nutritionist in a large company’s cafeteria has a guideline saying employees’ daily zinc intake should be about 14 mg/day. She selects a simple random sample of 70 employees and measures their zinc intake for one day. She finds their average intake is 13.8 mg. Earlier studies suggest that the population standard deviation of intakes is about 0.9 mg.

(a) Run a test, using significance level α = 0.05, to decide whether these data are stong evidence that the whole company population of employees took in too little zinc that day.
• Hypotheses:
• Assumptions:
• Test statistic:
• p-value:
• Conclusion:
(b) Suppose the population mean really was 14. Before sampling, what was the probability the test would reject H0 : µ = 14 even though it is true? Which type of error is this?

Answer 1

See below

Explanation:

a)

Hypothesis:

`\bf H_0`: The employees’ daily zinc intake is 14 mg.

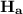`\bf H_a`: The employees’ daily zinc intake is less than mg.

So, this is a left-tailed test

Assumptions:

Population standard deviation of intakes

`\bf \sigma`= 0.9 mg.

Mean of the sample:

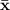`\bf \bar x`= 13.8

Mean of the population

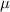`\bf \mu`= 14

Sample size

70

Test statistic:

`\bf z=(\bar x-\mu)/(\sigma/√(70))=(13.8-14)/(0.9/8.3666)=-1.8592`

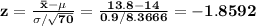
p-value:

This is the area under the Normal curve N(0,1) to the left of the test statistic -1.8592. Hence

p-value = 0.0315

Conclusion:

Since p-value<level of significance we reject
`\bf H_0`

(b) Suppose the population mean really was 14. Before sampling, what was the probability the test would reject H0 : µ = 14 even though it is true? Which type of error is this?

The probability the test would reject
`\bf H_0` is precisely the level of significance
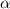`\bf \alpha`=0.05. So if we reject the null given that it is true, we would be making a Type 1 error.