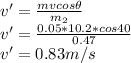Question

A system of inertia 0.47 kg consists of a spring gun attached to a cart and a projectile. The system is at rest on a horizontal low-friction track. A 0.050-kg projectile is loaded into the gun, then launched at an angle of 40∘ with respect to the horizontal plane.

Answer 1

v'=0.83m/a and v=10.2m/s

Step-by-step explanation:

The information that we have is:

`m_1=0.050kg\\m_2=0.47kg\\\theta = 40\\h=2.2m`

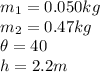
The maximum height of the projectile is given by the equation

`h=(v^2sin^2\theta)/(2g)`

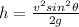
So, rearrange for the velocity,

`v=\sqrt{(2gh)/(sin^2\theta)}\\v=\sqrt{(2*9.8*2.2)/(sin^2(40))}\\v=10.2m/s`

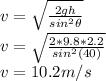
Apply the conservation of momentum,

`mvcos(\theta)=m'v'`

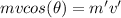
Then rearrange the recoil speed,

`v'=(mvcos\theta)/(m_2)\\v'=(0.05*10.2*cos40)/(0.47)\\v'=0.83m/s\\`