A 95% confidence interval for the true proportion of Gastown residents living below the poverty line is (0.1321, 0.2744).
In Mathematics and Statistics, the sample proportion of a sample can be calculated by using this formula:
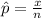
Where:
- x represent the total number of individuals that are having a specified characteristic.
- n represent the total number of individuals that are in the sample.
By substituting the given parameters, we have the following:
Sample proportion,
 = 25/123
= 25/123
Sample proportion,
 = 0.203252
= 0.203252
For a confidence level of 95%, the critical value of z is given by;
Critical value, z* = 1.960
Now, we can calculate the confidence interval (CI) by using the following formula;
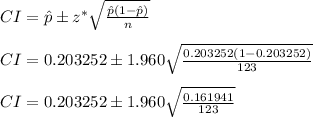
CI = (0.203252 ± 1.960(0.036285))
CI = (0.203252 ± 0.0711186)
CI = (0.203252 - 0.0711186, 0.203252 + 0.0711186)
CI = (0.1321, 0.2744)