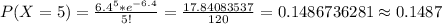Answer:
B) 0.1487
Explanation:
Let
 be the discrete random variable that represents the number of events observed over a given time period. If
be the discrete random variable that represents the number of events observed over a given time period. If
 follows a Poisson distribution, then the probability of observing
follows a Poisson distribution, then the probability of observing
 events over the time period is:
events over the time period is:
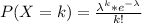
Where:

So, the probability that exactly 5 bankruptcies occur next month is: