Question

A particle moves along the curve y=7x2+8 in such a way that its x-coordinate is changing at a rate of 7 centimeters per second. At what rate is the particle's y-coordinate changing when the particle is at the point where x=−1x=−1?

Answer 1

The rate of change of the particle's y-coordinate when the particles is at the point x = −1 is
`(dy)/(dt)=-98 \:(cm)/(s)`

Explanation:

We know that the curve is described by
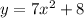`y=7x^(2)+8` and its x-coordinate is changing at a rate of 7 centimeters per second
`(dx)/(dt)=7 \:(cm)/(s)`

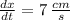
and we want to find the rate of change of the particle's y-coordinate (
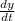`(dy)/(dt)`) when the particles is at the point x = −1.

First we need to find the derivative with respect of time of the curve
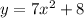`y=7x^(2)+8`, we use implicit differentiation.

`(d)/(dt) y=(d)/(dt)(7x^(2)+8)\\\\(dy)/(dt)=(d)/(dt)(7x^2)+(d)/(dt)(8)\\\\(dy)/(dt)=(d)/(dt)(7)x^2+7\cdot 2x(dx)/(dt) +0\\\\(dy)/(dt)=0\cdot x^2+14x(dx)/(dt)+0\\\\(dy)/(dt)=14x(dx)/(dt)`

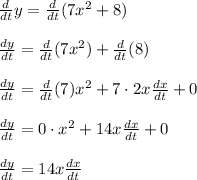
Now, we can substitute the values that we know

`(dx)/(dt)=7 \:(cm)/(s)`

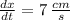
x = −1

`(dy)/(dt)=14x(dx)/(dt)\\\\(dy)/(dt)=14\cdot (-1)\cdot 7\\\\(dy)/(dt)=-98 \:(cm)/(s)`

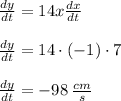
The rate of change of the particle's y-coordinate when the particles is at the point x = −1 is
`(dy)/(dt)=-98 \:(cm)/(s)`