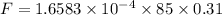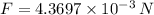Answer:
(a)
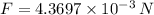
(b)
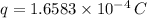
Step-by-step explanation:
Given:
- mass of positive charge,
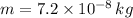
- speed of charge,
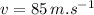
- magnetic field,
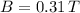
- time,
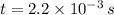
According to the given condition the positive charge enters due east and leaves the magnetic field heading due south completing one-quarter of a circle during the course of time during which it travels perpendicular to the magnetic field.
Now, by the Fleming's left hand rule we obtain that the direction of the field is outward of the plane in which the charge has traced the locus.
Firstly we find the angular velocity:
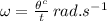
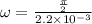
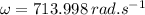
We know,
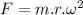 .........................(1)
.........................(1)
also
 .......................................(2)
.......................................(2)
from eq.(1) & (2)
(b)
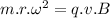
∵

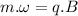
Putting the respective values in the above expression:
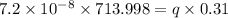
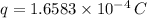
(a)
Putting the respective values in eq. (2)