Question

The daily revenue at a university snack bar has been recorded for the past five years. Records indicate that the mean daily revenue is $2700 and the standard deviation is $400. Suppose that 100 days are randomly selected. What is the probability that the average daily revenue of the sample is higher than $2600?

Answer 1

Answer: 0.9938

Explanation:

Let x be the random variable that represents the daily revenue at a university snack bar.

As per given , we have

`\mu=2700` ,
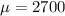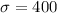`\sigma=400` and n= 100

Using formula
`z=(x-\mu)/((\sigma)/(√(n)))` ,

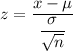z-score for x= 2600

`z=(2600-2700)/((400)/(√(100)))=-2.5`

The probability that the average daily revenue of the sample is higher than $2600 :

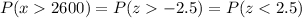`P(x>2600)=P(z>-2.5)=P(z<2.5)` [P(Z>-z)=P(Z<z)]

`=0.9937903\approx0.9938`

Therefore, the probability that the average daily revenue of the sample is higher than $2600 = 0.9938