Question

A 0.150 kg ball is fired from toy gun with a spring with spring constant k- 150 N/m, initially compressed by a distance x 0.050 m. The pellet's initial velocity is at an angle θ (θ < 90) above the horizontal. Assume no friction anywhere and assume that the acceleration of gravity g is constant. What is the final speed v of the projectile when it is at a distance h -0.800 m below its initial height (before it was launched)?

Answer 1

v = 4.264 m/s

Step-by-step explanation:

It is given that,

Mass of the ball, m = 0.15 kg

Spring constant of the spring, k = 150 N/m

The spring is compressed by a distance, x = 0.05 m

The pellet's initial velocity is at an angle θ (θ < 90) above the horizontal.

Let v is the final speed of the projectile when it is at a distance h = 0.800 m below its initial height. It can be calculated using the conservation of energy as :

`E_i=E_f`

`(1)/(2)kx^2+mgh=(1)/(2)mv^2`

`(1)/(2)* 150* (0.05)^2+0.15* 9.8* 0.8=(1)/(2)* 0.15* v^2`

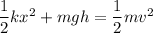
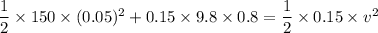
v = 4.264 m/s

So, the final speed of the projectile is 4.264 m/s. Hence, this is the required solution.