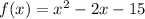What is the quadratic function for -3 and 5

Question

asked Mar 15, 2020 136k views

1 Answer

Sergei Kuraksin · Answer 1 · 2020-03-18T21:59:40+0000

For this case we have the following roots:

$x_ {1} = - 3\\x_ {2} = 5$

We must find a quadratic function associated with the given roots.

We have to, we can represent the solution as follows:

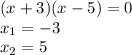
$(x + 3) (x-5) = 0\\x_ {1} = - 3\\x_ {2} = 5$

If we apply distributive property considering that:

+ * - = -

Different signs are subtracted and the major sign is placed.

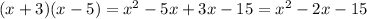
(x + 3) (x-5) = x ^ 2-5x + 3x-15 = x ^ 2-2x-15

Thus, the quadratic function is:

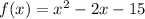
f (x) = x ^ 2-2x-15

Answer: