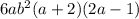Question

12a^3b^2 +18a²b^2 – 12ab^2
Factor completely

Answer 1

The factorization of 12a^3b^2 +18a²b^2 – 12ab^2 is
`6 a b^(2)(a+2)(2 a-1)`

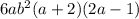
Solution:

Given, expression is
`12 a^(3) b^(2)+18 a^(2) b^(2)-12 a b^(2)`

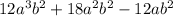
We have to factorize the given expression completely.

Now, take the expression

`12 a^(3) b^(2)+18 a^(2) b^(2)-12 a b^(2)`

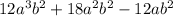
Taking
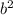`b^2` as common term,

`b^(2)\left(12 a^(3)+18 a^(2)-12 a\right)`

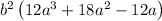
Taking "a" as common term,

`b^(2)\left(a\left(12 a^(2)+18 a-12\right)\right)`

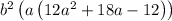
Taking "6" as common term,

`b^(2)\left(a\left(6\left(2 a^(2)+3 a-2\right)\right)\right)`

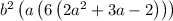
Splitting "3a" as "4a - a" we get,

`b^(2)\left(a\left(6\left(2 a^(2)+4 a-a-2\right)\right)\right)`

`\begin{array}{l}{b^(2)(a(6(2 a(a+2)-1(a+2))))} \\\\ {b^(2)(a(6((a+2) *(2 a-1))))} \\\\ {6 a b^(2)(a+2)(2 a-1)}\end{array}`

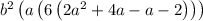
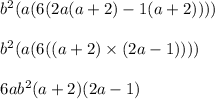
Hence, the factored form of given expression is
`6 a b^(2)(a+2)(2 a-1)`