Answer:
m₁ = 10.36 Kg
Step-by-step explanation:
Newton's second law:
∑F = m*a Formula (1)
∑F : algebraic sum of the forces in Newton (N)
m : mass in kilograms (kg)
a : acceleration in meters over second square (m/s²)
Calculating of the acceleration (a)
Because the masses moves with uniformly accelerated movement we apply the following formula:
vf²=v₀²+2*a*d Formula (2)
Where:
d:displacement in meters (m)
vi: initial speed in m/s
vf: final speed in m/s
a: acceleration in m/s²
Data:
vi = 0
vf = 3.5 m/s
d = 1.3 m
We replace data in the formula (2) to calculate the acceleration of the masses:
vf²=vi²+2*a*d
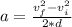
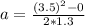
a= 4.7 m/s²
Problem development
m₁+m₂= 14.0 kg
g=9.81 m/s² acceleration due to gravity
W= m*g: Weight
- We identify a direction as positive and observe that m₁ will accelerate downwards and m₂ will accelerate upwards, since m₁> m₂.
Newton's second law for m₁:
We apply the formula (1)
We take + in the direction of the downward movement:
∑F = m*a
W₁ -T = m₁ *a
W₁- m₁ *a=T Equation (1)
Newton's second law for m₂:
We take + in the direction of the upward movement:
∑F = m*a
T-W₂ = m₂*a
T = W₂+m₂*a Equation (2)
Equation (1)=Equation (2) =T
W₁- m₁ *a = W₂+m₂*a
W₁- W₂ = m₁ *a + m₂*a
(m₁-m₂ )*g =a*( m₁ + m₂ ) m₁+ m₂ =14 , m₂ =14-m₁
(m₁-(14-m₁ )*9.8 = 4.7(14)
(m₁-14+m₁ )= ( 4.7((14) / (9.8)
2m₁ = 6.71 + 14
2m₁ = 20.71
m₁ = 10.36 Kg
m₂= 14 kg-10.36 kg
m₂= 3.64 kg