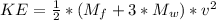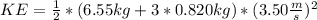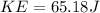Answer:
KE=55.18 J
Step-by-step explanation:
The angular velocity
ω
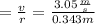
The moment of inertia of one solid disk bicycle wheel is
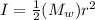
And the rotational kinetic energy of one wheel is
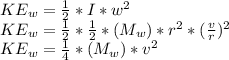
The total kinetic energy is then that of the frame and wheels plus the rotational kinetic energy.
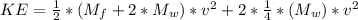
There is tow kinetic energy because are two wheels
Resolve