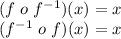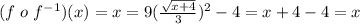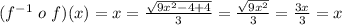Answer:
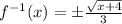
Explanation:
In order to find the inverse of
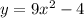 we need to follow the next steps:
we need to follow the next steps:
Step 1: Solve for x
Add 4 to both sides:
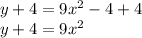
Divide by 9 from both sides:
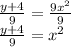
Square root from both sides:
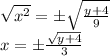
Step 2: Replace every x with a y and replace every y with an x.
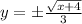
So:
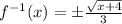
Step 3: Verify your work by checking that: