Question

For which function is the range y ?

a) f(x) = - x
b) f(x) = [[x]]
c) f(x) = | x |
d) f(x) = - | x |

Answer 1

d)
`f(x)=-|x|`

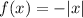
Explanation:

Given:

Range is,
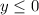`y\leq 0` which means range can be any real number less than or equal to 0.

Let us take
`x = -1` and test in all of the functions.

Consider the first function,
`f(x)=-x`.

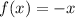So,
`f(-1)=-(-1) = 1`

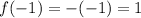
Here, range is greater than 0. So, option (a) is incorrect.

Consider the second function,
`f(x)=[[x]]`.

The second function is an integer value function whose range is only integers.

But, as per question, range can be any real number less than or equal to 0. Therefore, option (b) is also incorrect.

Consider the third function,
`f(x)=|x|`.

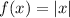For
`x= -1`,
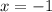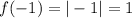`f(-1)=|-1|=1`. So, range is greater than 0.

Option (c) is also incorrect.

Consider the last function,
`f(x)=-|x|`.

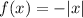For
`x= -1`,
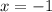`f(-1)=-|-1|=-1`. So, range is less than 0.

Option (d) is only correct.