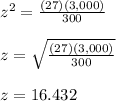Answer:
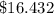
Explanation:
Let be "y" the monthly demand for the company’s sports caps, "x" the amount in dollar spent on advertising and "z"the price ind dollars per cap.
The model for this situation is:
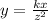
Where "k" is the constant of proportionality.
Since
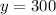 when
when
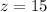 and
and
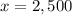 , we can substitute values into
, we can substitute values into
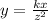 and solve for "k" to finds its value:
and solve for "k" to finds its value:

Then, in order to calculate what price yields a demand of 300 caps when advertising is increased to $3,000, we must substitute the following values into
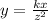 :
:

Then:
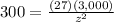
Solving for "z" we get: