Question

Suppose that f(x) = -2x4 + 5x3 - 7x - 4. Using only the Descartes' Rule of Signs, what are the possible number of positive zeros and the possible number of negative zeros?

Answer 1

2 or 0 Positive real roots; 2 Negative real roots

Explanation:

Consider the polynomial given:

`$ f(x) = - 2x^4 + 5x^3 +-7x - 4 $`

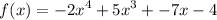
We see the signs of the co coefficients. They are
`$ -   +    -     - $`

`$ - \rightarrow + \rightarrow - \rightarrow - $`

The sign has changed two times. Negative to Positive and then positive to negative.

Descartes rule of sign says that the number of positive real roots is the number of times the sign has changed or difference between the number of changes in the sign and all the even numbers less than or equal to it.

Here the sign has changed two times. So, possible positive roots could be 2 or 2 - 2 = 0.

Now for the negative real roots, check for the changes in sign in
`$ f(-x) $`.

In this case, we would have:
`$ f(-x) = -2(-x)^4 + 5(-x)^3 -7(-x) - 4 $`

`$ \implies f(-x) = -2x^4 -5x^3 + 7x - 4 $`

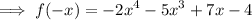
Clearly, the changes in the sign is 2. So we have two negative real roots.

Note that this equation has 4 roots.