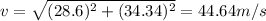Question

A ball is thrown horizontally from the top of a 60.0m and lands 100.0m from the base of the building ignore air resistance.(a) how long is the ball in the air? (b) what must have been the initial horizontal component of the velocity? (C) what is the vertical component of the velocity just before the ball hits the ground? (d) what is the velocity (including both the horizontal and velocity components) of the ball just before it hits the ground.

Answer 1

(a) 3.5 s

(b) 28.6 m/s

(c) 34.34 m/s

(d) 44.64 m/s

Step-by-step explanation:

(a)

`y=v_o t +0.5gt^(2)` where
`v_o` is initial velocity which is zero hence

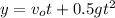`y=0.5gt^(2)` where t is time and g is acceleration due to gravity taken as 9.81 m/s2

Making t the subject,
`t=\sqrt {\frac {2y}{g}}`

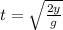
Substituting y for -60 m and g as -9.81 m/s2

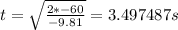`t=\sqrt {\frac {2*-60}{-9.81}}= 3.497487 s` and rounding off

t=3.5 s

(b)

Let
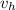`v_(h)` be horizontal component of velocity

Since the range
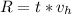`R=t*v_(h)` then making
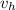`v_(h)` the subject

`v_(h)=\frac {R}{t}` and substituting R for 100m, t for 3.5 s then

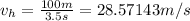`v_(h)=\frac {100 m}{3.5 s}= 28.57143 m/s` and rounding off

`v_(h)=28.6 m/s`

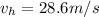
(c)

The vertical component of velocity before hitting ground

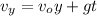`v_y=v_oy+ gt` but
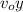`v_oy` is zero hence

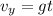`v_y=gt` and substituting g for -9.81 m/s2 and t for 3.5 s

`v_y=-9.81*3.5= -34.335` rounded off as -34.34 m/s

(d)

The velocity before it hits the ground will be

`v=\sqrt {(28.6)^(2)+(34.34)^(2)}=44.64 m/s`