The second person is walking faster than the first person.
Solution:
Given, One person walks
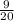 miles in each
miles in each
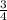 hour.
hour.
Another person walks
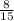 miles in each
miles in each
 hour.
hour.
We have to find who is walking faster?
Now, we know that, distance = speed x time
Let us find the speed of each person
Speed of first person:

Speed of second person:

We know that,
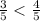
Hence, the second person is walking faster than the first person.