Question

what is the equation in slope intercept form of the line that goes through (2,4) and is perpendicular to the line represented by y=-2/3x+6

Answer 1

`y = (3x)/(2)+1`

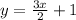
Explanation:

The slope-intercept form of a straight line equation is y = mx + c, where m is the slope and c is the y-intercept of the line.

Now, we know that if two straight lines are perpendicular to each other then the product of their slopes will be -1.

So, the equation of a straight line which is perpendicular to the line
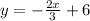`y = -(2x)/(3) +6` will be
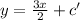`y= (3x)/(2)+ c'` ....... (1), where c' is constant.

Given that the line (1) passes through (2,4) point.

Hence,
`4 = (3(2))/(2) +c'`

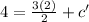
⇒ c' = 1.

Therefore, the final equation of the required straight line is
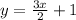`y = (3x)/(2)+1`. (Answer)