For this case we have that by definition, the discriminant of a quadratic expression is given by:

If the discriminant is less than zero then the expression has two different complex roots.
In this case we have the following expression:
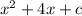
So we have to:
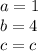
The discriminant is given by:
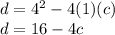
Then, if we want two complex roots it must be fulfilled that:
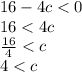
Thus, the expression has two complex roots for all values greater than 4.
ANswer:
